Sigmoid-Aktivierungsfunktion Tutorial

In diesem Tutorial werden wir die Sigmoid-Aktivierungsfunktion kennenlernen. Die Sigmoid-Funktion liefert immer einen Ausgabewert zwischen 0 und 1.

Nach diesem Tutorial wirst du wissen:

• Was ist eine Aktivierungsfunktion?
• Wie implementiert man die Sigmoid-Funktion in Python?
• Wie stellt man die Sigmoid-Funktion in Python dar?
• Wo wird die Sigmoid-Funktion verwendet?
• Welche Probleme verursacht die Sigmoid-Aktivierungsfunktion?
• Bessere Alternativen zur Sigmoid-Aktivierung.

Was ist eine Aktivierungsfunktion?

Eine Aktivierungsfunktion ist eine mathematische Funktion, die den Ausgang eines neuronalen Netzwerks steuert. Aktivierungsfunktionen helfen dabei zu bestimmen, ob ein Neuron aktiviert wird oder nicht.

Beliebte Aktivierungsfunktionen

• Binärer Schritt
• Linear
• Sigmoid
• Tanh
• ReLU
• Leaky ReLU
• Softmax

Aktivierung ist verantwortlich für das Hinzufügen von Nichtlinearität zum Ausgang eines neuronalen Netzwerkmodells. Ohne eine Aktivierungsfunktion ist ein neuronales Netzwerk lediglich eine lineare Regression.

Sigmoid-Aktivierungsfunktion Formel

Die mathematische Gleichung zur Berechnung des Ausgangs eines neuronalen Netzwerks ist:

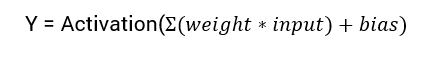Aktivierungsfunktion

In diesem Tutorial konzentrieren wir uns auf die Sigmoid-Aktivierungsfunktion. Diese Funktion stammt von der Sigmoid-Funktion in der Mathematik.

Die Formel für die Sigmoid-Aktivierungsfunktion

Mathematisch kann man die Sigmoid-Aktivierungsfunktion darstellen als:

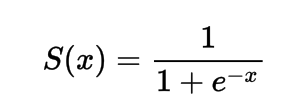
Formel

Man kann sehen, dass der Nenner immer größer als 1 sein wird, daher wird der Ausgang immer zwischen 0 und 1 liegen.

Implementierung der Sigmoid-Aktivierungsfunktion in Python

In diesem Abschnitt werden wir lernen, wie man die Sigmoid-Aktivierungsfunktion in Python implementiert.

    import numpy as np 
    def sig(x):
        return 1/(1 + np.exp(-x))

    import numpy as np 
    def sig(x):
        return 1/(1 + np.exp(-x))

    x = 1.0
    print('Anwendung der Sigmoid-Aktivierung auf (%.1f) ergibt %.1f' % (x, sig(x)))

    x = -10.0
    print('Anwendung der Sigmoid-Aktivierung auf (%.1f) ergibt %.1f' % (x, sig(x)))

    x = 0.0
    print('Anwendung der Sigmoid-Aktivierung auf (%.1f) ergibt %.1f' % (x, sig(x)))

    x = 15.0
    print('Anwendung der Sigmoid-Aktivierung auf (%.1f) ergibt %.1f' % (x, sig(x)))

    x = -2.0
    print('Anwendung der Sigmoid-Aktivierung auf (%.1f) ergibt %.1f' % (x, sig(x)))

• Anwendung der Sigmoid-Aktivierung auf (1.0) ergibt 0.7
• Anwendung der Sigmoid-Aktivierung auf (-10.0) ergibt 0.0
• Anwendung der Sigmoid-Aktivierung auf (0.0) ergibt 0.5
• Anwendung der Sigmoid-Aktivierung auf (15.0) ergibt 1.0
• Anwendung der Sigmoid-Aktivierung auf (-2.0) ergibt 0.1

Zeichnen der Sigmoid-Aktivierung mit Python

Um die Sigmoid-Aktivierung zu zeichnen, verwenden wir die Numpy-Bibliothek:

    import numpy as np
    import matplotlib.pyplot as plt
    x = np.linspace(-10, 10, 50)   
    p = sig(x)
    plt.xlabel("x") 
    plt.ylabel("Sigmoid(x)")  
    plt.plot(x, p) 
    plt.show()

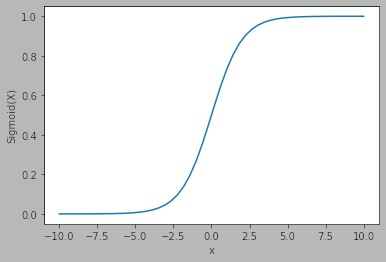Sigmoid

Wir können sehen, dass der Ausgang zwischen 0 und 1 liegt.

Die Sigmoid-Funktion wird häufig verwendet, um Wahrscheinlichkeiten vorherzusagen, da die Wahrscheinlichkeit immer zwischen 0 und 1 liegt.

Einer der Nachteile der Sigmoid-Funktion ist, dass sich die Y-Werte in den Endregionen sehr wenig in Bezug auf die Änderungen der X-Werte ändern.

Dies führt zu einem Problem, das als das Problem des verschwindenden Gradienten bekannt ist.

Ein verschwindender Gradient verlangsamt den Lernprozess und ist daher unerwünscht.

Alternativen zur Sigmoid-Aktivierungsfunktion

ReLu-Aktivierungsfunktion

Eine bessere Alternative, die dieses Problem des verschwindenden Gradienten löst, ist die ReLu-Aktivierungsfunktion.

Die ReLu-Aktivierungsfunktion gibt 0 zurück, wenn der Eingang negativ ist, sonst gibt sie den Eingang so zurück, wie er ist.

Mathematisch wird es dargestellt als:

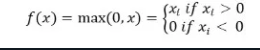Relu

Sie können es in Python wie folgt implementieren:

    def relu(x):
        return max(0.0, x)

    def relu(x):
        return max(0.0, x)

    x = 1.0
    print('Anwendung von Relu auf (%.1f) ergibt %.1f' % (x, relu(x)))
    x = -10.0
    print('Anwendung von Relu auf (%.1f) ergibt %.1f' % (x, relu(x)))
    x = 0.0
    print('Anwendung von Relu auf (%.1f) ergibt %.1f' % (x, relu(x)))
    x = 15.0
    print('Anwendung von Relu auf (%.1f) ergibt %.1f' % (x, relu(x)))
    x = -20.0
    print('Anwendung von Relu auf (%.1f) ergibt %.1f' % (x, relu(x)))

• Anwendung von Relu auf (1.0) ergibt 1.0
• Anwendung von Relu auf (-10.0) ergibt 0.0
• Anwendung von Relu auf (0.0) ergibt 0.0
• Anwendung von Relu auf (15.0) ergibt 15.0
• Anwendung von Relu auf (-20.0) ergibt 0.0

Leaky ReLu-Aktivierungsfunktion

Die Leaky ReLu adressiert das Problem von Nullgradienten bei negativen Werten, indem sie einen extrem kleinen linearen Anteil von x für negative Eingaben bereitstellt.

Mathematisch können wir es definieren als:

f(x) = 0.01x, x < 0

f(x) = x, x ≥ 0

Sie können es in Python wie folgt implementieren:

    def leaky_relu(x):
        if x > 0 :
            return x
        else :
            return 0.01*x

    x = 1.0
    print('Anwendung von Leaky Relu auf (%.1f) ergibt %.1f' % (x, leaky_relu(x)))

    x = -10.0
    print('Anwendung von Leaky Relu auf (%.1f) ergibt %.1f' % (x, leaky_relu(x)))

    x = 0.0
    print('Anwendung von Leaky Relu auf (%.1f) ergibt %.1f' % (x, leaky_relu(x)))

    x = 15.0
    print('Anwendung von Leaky Relu auf (%.1f) ergibt %.1f' % (x, leaky_relu(x)))

    x = -20.0
    print('Anwendung von Leaky Relu auf (%.1f) ergibt %.1f' % (x, leaky_relu(x)))

• Anwendung von Leaky Relu auf (1.0) ergibt 1.0
• Anwendung von Leaky Relu auf (-10.0) ergibt -0.1
• Anwendung von Leaky Relu auf (0.0) ergibt 0.0
• Anwendung von Leaky Relu auf (15.0) ergibt 15.0
• Anwendung von Leaky Relu auf (-20.0) ergibt -0.2

Schlussfolgerung

Dieses Tutorial handelte von der Sigmoid-Aktivierungsfunktion. Wir haben gelernt, wie man die Funktion in Python implementiert und darstellt.