N-Queens-Problem: Lösen mit Backtracking in Java/C++
Wenn du gerne Schach spielst, wirst du es genießen, über das N-Queens-Problem zu lernen. Es ist ein gutes Problem, um Backtracking zu verstehen.
Was ist Backtracking?
Beim Backtracking starten wir mit einem möglichen Zug aus vielen verfügbaren Zügen. Dann versuchen wir, das Problem zu lösen.
Wenn wir das Problem mit dem ausgewählten Zug lösen können, drucken wir die Lösung. Andernfalls gehen wir zurück und wählen einen anderen Zug und versuchen, es zu lösen.
Wenn keiner der Züge funktioniert, behaupten wir, dass es keine Lösung für das Problem gibt.
Was ist das N-Queens-Problem?
Wie können N Queens auf einem NxN Schachbrett platziert werden, sodass sich keine zwei davon angreifen?
Dieses Problem wird häufig für N=4 und N=8 gesehen.
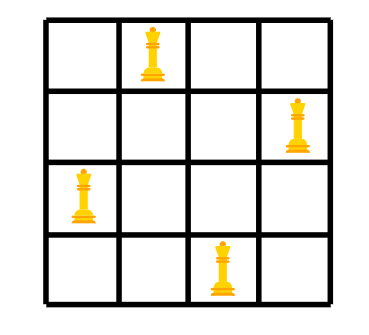
Lassen Sie uns ein Beispiel betrachten, wo N=4 ist
Bevor wir das Problem lösen, müssen Sie über die Bewegung der Königin im Schach wissen.
Eine Königin kann beliebig viele Schritte in jede Richtung machen. Die einzige Einschränkung ist, dass sie ihre Richtung während der Bewegung nicht ändern kann.
Eine Sache, die beim Betrachten der Bewegung der Königin klar wird, ist, dass keine zwei Königinnen in derselben Reihe oder Spalte sein können.
Dadurch können wir nur eine Königin in jeder Reihe und jeder Spalte platzieren.
Wenn N=4 ist, sieht die Lösung so aus:

Aber wie kommen wir zu dieser Anordnung?
Lösung des N-Queens-Problems
Die Art und Weise, wie wir dies zu lösen versuchen, besteht darin, eine Königin an einer Position zu platzieren und zu versuchen, die Möglichkeit auszuschließen, dass sie angegriffen wird. Wir platzieren eine Königin in jeder Reihe/Spalte.
Wenn wir sehen, dass die Königin an ihrer gewählten Position angegriffen wird, versuchen wir die nächste Position.
Wenn eine Königin an allen Positionen in einer Reihe angegriffen wird, gehen wir zurück und ändern die Position der zuvor platzierten Königin.
Wir wiederholen diesen Prozess des Platzierens einer Königin und des Zurückgehens, bis alle N Königinnen erfolgreich platziert sind.
Das schrittweise Backtracking wird wie folgt gezeigt:
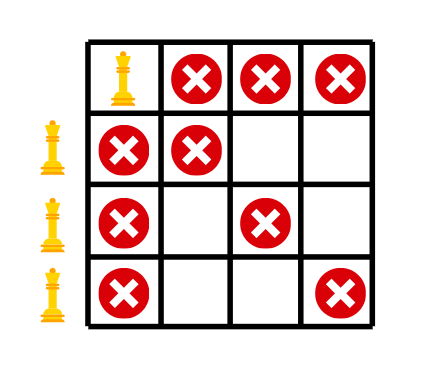
Das rote Kreuz markiert die Positionen, die von einer Königin angegriffen werden. Wann immer wir einen Zustand erreichen, in dem wir eine Königin platzieren müssen, aber alle Positionen in den Reihen angegriffen werden, gehen wir zurück.
Dies ist nicht die einzige mögliche Lösung für das Problem. Wenn Sie jede Königin einen Schritt vorwärts im Uhrzeigersinn bewegen, erhalten Sie eine weitere Lösung.
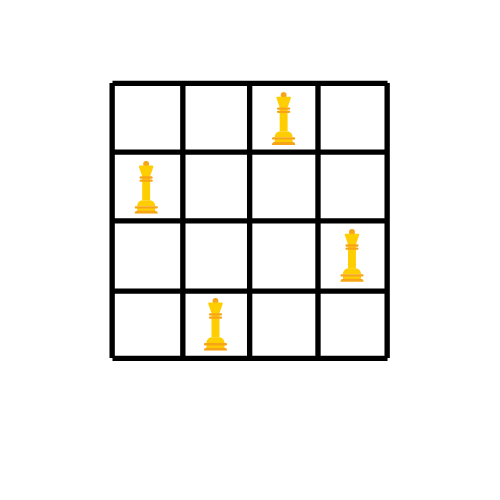
In diesem Beispiel haben wir die Königinnen nach Reihen platziert, wir können dasselbe auch spaltenweise tun. In diesem Fall würde jede Königin zu einer Spalte gehören.
Implementierung des N-Queens-Problems in C++ und Java
Implementierung des N-Queens-Problems in C++:
#define N 4
#include <stdbool.h>
#include <stdio.h>
//function to print the solution
void printSolution(int board[N][N])
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
printf(" %d ", board[i][j]);
printf("\n");
}
}
// function to check whether the position is safe or not
bool isSafe(int board[N][N], int row, int col)
{
int i, j;
for (i = 0; i < col; i++) if (board[row][i]) return false; for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j])
return false;
for (i = row, j = col; j >= 0 && i < N; i++, j--) if (board[i][j]) return false; return true; } // The function that solves the problem using backtracking bool solveNQUtil(int board[N][N], int col) { if (col >= N)
return true;
for (int i = 0; i < N; i++) { //if it is safe to place the queen at position i,col -> place it
if (isSafe(board, i, col)) {
board[i][col] = 1;
if (solveNQUtil(board, col + 1))
return true;
board[i][col] = 0; // BACKTRACK
}
}
return false;
}
// driver program to test above function
int main()
{
int board[N][N] = { { 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 } };
if (solveNQUtil(board, 0) == false) {
printf("Solution does not exist");
return 0;
}
printSolution(board);
return true;
return 0;
}
Implementierung des N-Queens-Problems in Java:
package com.JournalDev;
public class Main {
static final int N = 4;
// print the final solution matrix
static void printSolution(int board[][])
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
System.out.print(" " + board[i][j]
+ " ");
System.out.println();
}
}
// function to check whether the position is safe or not
static boolean isSafe(int board[][], int row, int col)
{
int i, j;
for (i = 0; i < col; i++) if (board[row][i] == 1) return false; for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j] == 1)
return false;
for (i = row, j = col; j >= 0 && i < N; i++, j--) if (board[i][j] == 1) return false; return true; } // The function that solves the problem using backtracking public static boolean solveNQueen(int board[][], int col) { if (col >= N)
return true;
for (int i = 0; i < N; i++) { //if it is safe to place the queen at position i,col -> place it
if (isSafe(board, i, col)) {
board[i][col] = 1;
if (solveNQueen(board, col + 1))
return true;
//backtrack if the above condition is false
board[i][col] = 0;
}
}
return false;
}
public static void main(String args[])
{
int board[][] = { { 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 } };
if (!solveNQueen(board, 0)) {
System.out.print("Solution does not exist");
return;
}
printSolution(board);
}
}
Output :
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
For N=8 the output is :
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
Verständnis der Code-Implementierung
Um zu überprüfen, ob eine Position angegriffen wird oder nicht, haben wir eine Funktion namens isSafe erstellt.
Die Funktion gibt true zurück, wenn die Positionen sicher vor jedem Angriff sind.
static boolean isSafe(int board[][], int row, int col)
{
int i, j;
for (i = 0; i < col; i++) if (board[row][i] == 1) return false; for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j] == 1)
return false;
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j] == 1)
return false;
return true;
}
Die erste for-Schleife prüft entlang der Spalte, die zweite und dritte for-Schleifen prüfen entlang der beiden Diagonalen.
Der folgende Codeausschnitt ist dafür verantwortlich, die Königinnen an ihrer Position zu platzieren und zurückzugehen. Um die Position einer Königin zu markieren, setzen wir diese Zelle als 1 im Matrix. Bevor wir die Königin platzieren, rufen wir isSafe auf, um sicherzustellen, dass die Position sicher ist.
public static boolean solveNQueen(int board[][], int col)
{
if (col >= N)
return true;
for (int i = 0; i < N; i++) { //if it is safe to place the queen at position i,col -> place it
if (isSafe(board, i, col)) {
board[i][col] = 1;
if (solveNQueen(board, col + 1))
return true;
//backtrack if the above condition is false
board[i][col] = 0;
}
}
return false;
}
Der rekursive Aufruf übergibt das Board und setzt die Spalte auf col+1. Wenn der rekursive Aufruf false zurückgibt, gehen wir zurück, indem wir den Eintrag auf 0 zurücksetzen.
Schlussfolgerung
So lösen Sie das N-Queen-Problem mit Backtracking.


